Interview Review Material
- Things left to study
- Probability
- Calculus
- Linear Algebra
- Misc Math Concepts
- Computer Science
- Languages
- Machine Learning
- Supervised, self-supervised, semi-supervised, unsupervised learning
- Linear Regression
- Logistic Regression
- Gradient Descent
- Convergence Guarantees
- Features
- Bias and variance in learning
- Generalization
- Over-fitting and Under-fitting
- Regularization
- Evaluating methods
- Support Vector Machines
- Kernel Methods
- Artificial Neural Networks
- Boosting
- Bagging
- Ensemble methods
- Principle Component Analysis
- Advanced Neural Network Examples
- Questions
- Reinforcement Learning
- HR/personality Interviews
- Research Topics
- Potential Interview Questions
- References
\( \newcommand{\states}{\mathcal{S}} \newcommand{\actions}{\mathcal{A}} \newcommand{\observations}{\mathcal{O}} \newcommand{\rewards}{\mathcal{R}} \newcommand{\traces}{\mathbf{e}} \newcommand{\transition}{P} \newcommand{\reals}{\mathbb{R}} \newcommand{\naturals}{\mathbb{N}} \newcommand{\complexs}{\mathbb{C}} \newcommand{\field}{\mathbb{F}} \newcommand{\numfield}{\mathbb{F}} \newcommand{\expected}{\mathbb{E}} \newcommand{\var}{\mathbb{V}} \newcommand{\by}{\times} \newcommand{\partialderiv}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\defineq}{\stackrel{{\tiny\mbox{def}}}{=}} \newcommand{\defeq}{\stackrel{{\tiny\mbox{def}}}{=}} \newcommand{\eye}{\Imat} \newcommand{\hadamard}{\odot} \newcommand{\trans}{\top} \newcommand{\inv}{{-1}} \newcommand{\argmax}{\operatorname{argmax}} \newcommand{\Prob}{\mathbb{P}} \newcommand{\avec}{\mathbf{a}} \newcommand{\bvec}{\mathbf{b}} \newcommand{\cvec}{\mathbf{c}} \newcommand{\dvec}{\mathbf{d}} \newcommand{\evec}{\mathbf{e}} \newcommand{\fvec}{\mathbf{f}} \newcommand{\gvec}{\mathbf{g}} \newcommand{\hvec}{\mathbf{h}} \newcommand{\ivec}{\mathbf{i}} \newcommand{\jvec}{\mathbf{j}} \newcommand{\kvec}{\mathbf{k}} \newcommand{\lvec}{\mathbf{l}} \newcommand{\mvec}{\mathbf{m}} \newcommand{\nvec}{\mathbf{n}} \newcommand{\ovec}{\mathbf{o}} \newcommand{\pvec}{\mathbf{p}} \newcommand{\qvec}{\mathbf{q}} \newcommand{\rvec}{\mathbf{r}} \newcommand{\svec}{\mathbf{s}} \newcommand{\tvec}{\mathbf{t}} \newcommand{\uvec}{\mathbf{u}} \newcommand{\vvec}{\mathbf{v}} \newcommand{\wvec}{\mathbf{w}} \newcommand{\xvec}{\mathbf{x}} \newcommand{\yvec}{\mathbf{y}} \newcommand{\zvec}{\mathbf{z}} \newcommand{\Amat}{\mathbf{A}} \newcommand{\Bmat}{\mathbf{B}} \newcommand{\Cmat}{\mathbf{C}} \newcommand{\Dmat}{\mathbf{D}} \newcommand{\Emat}{\mathbf{E}} \newcommand{\Fmat}{\mathbf{F}} \newcommand{\Gmat}{\mathbf{G}} \newcommand{\Hmat}{\mathbf{H}} \newcommand{\Imat}{\mathbf{I}} \newcommand{\Jmat}{\mathbf{J}} \newcommand{\Kmat}{\mathbf{K}} \newcommand{\Lmat}{\mathbf{L}} \newcommand{\Mmat}{\mathbf{M}} \newcommand{\Nmat}{\mathbf{N}} \newcommand{\Omat}{\mathbf{O}} \newcommand{\Pmat}{\mathbf{P}} \newcommand{\Qmat}{\mathbf{Q}} \newcommand{\Rmat}{\mathbf{R}} \newcommand{\Smat}{\mathbf{S}} \newcommand{\Tmat}{\mathbf{T}} \newcommand{\Umat}{\mathbf{U}} \newcommand{\Vmat}{\mathbf{V}} \newcommand{\Wmat}{\mathbf{W}} \newcommand{\Xmat}{\mathbf{X}} \newcommand{\Ymat}{\mathbf{Y}} \newcommand{\Zmat}{\mathbf{Z}} \newcommand{\Sigmamat}{\boldsymbol{\Sigma}} \newcommand{\identity}{\Imat} \newcommand{\epsilonvec}{\boldsymbol{\epsilon}} \newcommand{\thetavec}{\boldsymbol{\theta}} \newcommand{\phivec}{\boldsymbol{\phi}} \newcommand{\muvec}{\boldsymbol{\mu}} \newcommand{\sigmavec}{\boldsymbol{\sigma}} \newcommand{\jacobian}{\mathbf{J}} \newcommand{\ind}{\perp!!!!\perp} \newcommand{\bigoh}{\text{O}} \)
This document is meant as a source to review material for studying for machine learning interviews. I’m hoping the construction of this document will help in reviewing the basics, and fortify the foundations of my own notebase.
Things left to study
- Finish anki cards [hard]
- Lots of ML concepts to remember still…
- Deep Learning Book
- Fill out the rest of the following note pages…
- Go through problems in this book [hard]
- Linear regression and its assumptions [easy] (see Linear Regression)
- Practice deriving MLE and MAP estimators [medium] (see MLE for partial review, still need to fill out).
- Backpropagation
- WTF is LDA again? Linear discriminate analysis.
- Read and brush up on Support Vector Machines [medium] Support Vector Machines
- Naive Bayes [easy]
- Kernels and kernel functions
- What is a RKHS again??
- Kernel funcs
- Probability examples!!!!!
- XGBoost
- Code:
- Naive Bayes
- SVMs
- Logistic Regression
- MC for calculating pi
- Linear Regression, Lasso, and Ridge regression.
- EM for GMMs
- RL
- Off-policy vs on-policy, some off-policy algs.
- Exploration vs exploitation
- Options and temporal abstractions
- Policy Evaluation, Value Iteration, Policy Iteration oh my!
- Traces
- Why/when does SGD converge???
- More on hypothesis testing and more complex tests.
- Graphs and Causality!!!
- Box-cox transformation??? - deals with skewness??
- Jensen’s Inequality
Probability
First lets define some basic objects for thinking about the world probabilistically. For an event space \(\Sigma\) with events sampled from that space \(A \in \Sigma\). We assign a real value \(\Prob(A) \in \reals\) to every event in the space and call \(\Prob\) a probability distribution or probability measure if it follows the following axioms:
- \(\Prob(A) \geq 0 \forall A\)
- \(\Prob(\Sigma) = \sum_{A \in \Sigma} \Prob(A) = 1\)
- If the events are disjoint then
\[\Prob(\cup_{i} A_i) = \sum_i \Prob(A_i)\]
A Random Variable is a mapping from outcome spaces to real numbers \(X: \Sigma \rightarrow \reals\) that assigns a real value to \(X(\omega)\) to each outcome \(\omega\).
Given a random variable \(X\) we can define the cumulative distribution function (CDF) \(F_X: \reals \rightarrow [0, 1]\) of a random variable \(X\) is defined by \[ F_X(x) = \Prob(X \leq x) \]
(Example from (Wasserman 2004)) Flip a fair coin twice and let \(X\) be the number of heads. Then \(\Prob(X=0)=\Prob(X=2) = \frac{1}{4}\) and \(\Prob(X=1) = \frac{1}{2}\). The distribution function is \[ F_{X}(x) = \begin{cases} 0 \quad &x<0 \\ \frac{1}{4} \quad &0 \leq x < 1 \\ \frac{3}{4} \quad &1 \leq x < 2 \\ 1 \quad &x \geq 2. \end{cases} \]
A function F which maps the real line to \([0, 1]\) is a CDF if and only if:
- F is non-decreasing: \(x_1 < x_2 \rightarrow F(x_1) \leq F(x_2)\)
- F is normalized: \(\lim_{x\rightarrow-\infty} F(x) = 0\) and \(\lim_{x\rightarrow\infty} F(x) = 1\)
- F is right continuous: \(F(x) = F(x^+)\) where \(x^+\) implies approaching \(x\) from above.
We must define two probability functions depending on whether the random variable \(X\) is discrete or continuous. If the variable is discrete then we define the probability mass function for \(X\) by \[ f_X(x) = \Prob(X=x). \]
If the random variable \(X\) is continuous if there exits a function \(f_X\) such that
- \(f_X(x) \geq 0 \forall x \in X\)
- \(\int_{-\infty}^{\infty} f_X(x)dx = 1\)
- and for every \(a \leq b\) \[ \Prob(x < X < b) = \int_a^b f_X(x)dx. \]
The function \(f_X\) is called a probability density function we have that \[ F_X(x) = \int_{-\infty}^{x} f_X(t)dt \]
and \(f_X(x) = F^\prime_X(x)\) at all points \(x\) at which \(F_X\) is differentiable.
Expectations of a random variable
The expected value, or mean, or first moment of \(X\) is defined to be \[ \expected(X) = \int x dF(x) = \begin{cases} \sum_x xf(x) \quad &\text{if $X$ is discrete}\\ \int xf(x)dx \quad &\text{if $X$ is continuous} \end{cases} \] assuming that the sum (or integral) is well-defined.
Some properties:
- If \(X_1, \ldots, X_2\) are random variables and \(a_1, \ldots, a_n\) are constants, then \[\expected\left(\sum_i a_i X_i \right) = \sum_i a_i \expected(X_i).\]
- Let \(X_1, \ldots, X_2\) be independent random variables. Then, \[\expected\left(\prod_{i=1}^n X_i \right) = \prod_i \expected(X_i)\]
The variance of a distribution is the “spread” of the distribution. The variance of a random variable \(X\) with mean \(\mu\) is defined by \[ \sigma^2 = \var(X) = \expected(X-\mu)^2= \int (x-\mu)^2 dF(x) \]
assuming this expectation exists. The standard deviation is \(sd(X) = \sqrt{\var(X)}\). The variance has the following properties:
- \(\var(X) = \expected(X^2) - \mu^2\).
- If \(a\) and \(b\) are constants then \(\var(aX + b) = a^2\var(X)\).
- If \(X_1,\ldots,X_n\) are independent and \(a_1,\ldots,a_n\) are constants, then \[\var\left(\sum_{i=1}^n a_i X_i \right) = \sum_{i=1}^n a_i^2 \var(X_i)\].
If X and Y are random variables with means \(\mu_X\) and \(\mu_Y\) and standard deviations \(\sigma_X\) and \(\sigma_Y\), the covariance between \(X\) and \(Y\) is defined as \[\text{Cov}(X, Y) = \expected[(X-\mu_X)(Y-\mu_Y)]\] and the correlation by \[\rho_{X, Y} = \rho(X, Y) = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y}\]
Moments of a random variable
The nth-moment of a random variable is defined as: \[ \mu_n = \expected[(X - c)^n] = \int_{-\infty}^{\infty} (x-c)^n f(x) dx \]
The raw moment is defined as the moment centered around zero (i.e. \(c=0\) above). The first raw moment is the mean of the random variable. We can also define the central moments by setting \(c=\mu\) or the the center of the moment to the mean of the random variable. \[ \expected[(X-\expected[X])^n] \] The second central moment is the variance. Finally, we can normalize the moment by powers of the standard deviation creating standardized moments \[ \expected[\frac{(X-\expected[X])^n}{\sigma^2}] \] where \(\sigma=\sqrt{\var(X)}\) is the standard deviation.
The skewness and kurtosis are the 3rd and 4th standardized moments respectively. The skewness of a distribution is how “skewed” or asymmetric it is around the mean. This gives an indication on where the tail is in a unimodal distribution (i.e. left or right side). The kurtosis describes how much “tail” the distribution has, or its “tailedness”.
Basic Inequalities
There are a few basic inequalities that everyone should know imho.
Let \(X\) be a non-negative random variable and suppose that \(\expected(X)\) exists. For any t>0 \[\Prob(X>t) \leq \frac{\expected(X)}{t}.\]
Let \(\mu = \expected(X)\) and \(\sigma^2 = \var(X)\). Then \[\Prob(|X-\mu| \geq t) \leq \frac{\sigma^2}{t^2} \text{ and } \Prob(|Z|\geq k)\leq\frac{1}{k^2}\] where \(Z = \frac{(X-\mu)}{\sigma}\). In particular, \(\Prob(|Z| > 2)\leq \frac{1}{4}\) and \(\Prob(|Z| > 3) \leq \frac{1}{9}\).
Classical convergence theorems of random variables
There are a few classic results that are important when thinking about probability and statistics in learning theory.
The law of large numbers says that sample average \(\bar{X}_n = n^\inv \sum_{i=1}^n X_i\) converges in probability to the expectation \(\mu = \expected(X)\).
The law of large number tells us that as we sample from our data more, the sample average will converge to the actual expected value. This means that if we want a better estimate an easy solution is to gather more data, and this has been a common theme in recent machine learning research (i.e. Deep Learning soaks up data).
The central limit theorem says that sample average has approximately a Normal distribution for large \(n\). More exact, \(\sqrt{n}(\bar{X}_n - \mu)\) converges in distribution to a \(\text{Normal}(0, \sigma^2)\) distribution, where \(\sigma^2 = \var(X)\).
The central limit theorem gives us a way to reason about the variance of the sample averages. Because the random variable defined by the sample average will be distributed according \(\text{Normal}(\mu, \sigma^2)\) we can estimate the confidence intervals for our current estimate.
Hypothesis testing and p-values
Hypothesis testing is at the core of empirical science, which is a core facet of todays Machine Learning research. Hypothesis testing gives us the ability to (with some certainty) measure differences or changes made by experimental interventions. For two methods, say one baseline and one new method designed by the scientist we test two hypotheses simultaneously:
- The Null Hypothesis: The two algorithms perform the same.
- The Alternative Hypothesis: The two algorithms do not perform the same.
Our hope is that the null hypothesis can be rejected given the data collected (i.e. if the new algorithm considerably under or overperforms the baseline).
Some Discrete Distributions
-
Bernoulli
Bernoulli distribution is that of a biased coin flip with a probability of getting heads (or a success) set to \(\alpha\). For a random variable \(X \in \{0, 1\}\) we define the Bernoulli distribution as: \[X \sim \text{Bernoulli}(\alpha) \rightarrow \Prob(X=x) = \alpha^x (1-\alpha)^{1-x} \]
where the mean is \(\alpha\) and variance is \(\alpha(1-\alpha)\).
-
Binomial
The binomial distribution is the probability of k successes in n trials of random pulls from the Bernoulli distribution. \[X\sim \text{Binomial}(\alpha, n) \rightarrow \Prob(X=k; \alpha, n) = \frac{n!}{k! (n-k)!} \alpha^k (1-\alpha)^{n-k}\]
where the mean is \(n\alpha\) and the variance is \(n\alpha(1-\alpha)\)
-
Geometric
The geometric distribution is how many trials we need to see before we see a successful trial. \[X\sim \text{Geometric}(\alpha) \rightarrow \Prob(X=k; \alpha)=\alpha(1-\alpha)^{k-1}\]
with mean \(\frac{1}{\alpha}\) and variance \(\frac{1-\alpha}{\alpha^2}\).
-
Poisson
The Poisson distribution is the probability of seeing k independent events in a set interval with a rate \(\lambda\). \[X \sim \text{Poisson}(\lambda) \rightarrow \Prob(X=k; \lambda) = \frac{\lambda^k e^{-\lambda}}{k!}\]
where the mean and variance is \(\lambda\).
Some Continual Distributions
-
Normal
The normal (or gaussian) distribution is used quite often. For mean \(\mu\) and variance \(\sigma^2\)
\[X \sim \text{Normal}(\mu, \sigma^2) \rightarrow f_X(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]
-
Laplace
The Laplace distribution is like two exponentials centered on the mean.
\[X \sim \text{Laplace}(\mu, b) \rightarrow f_X(x) = \frac{1}{2b} e^{-\frac{\lvert x - \mu \rvert}{b}}\]
with mean \(\mu\) and variance \(2b^2\).
-
Gamma
The gamma distribution is \[X \sim \text{Gamma}(\alpha, \beta) \rightarrow f_X(x) = x^{\alpha-1} e^{-\beta x} \frac{\beta^\alpha}{\Gamma(\alpha)}\]
with mean \(\frac{\alpha}{\beta}\) and variance \(\frac{\alpha}{\beta^2}\)
Questions
- Central limit theorem
- Different kinds of probability distributions and when you would use them?
- What is PDF and CDF?
- What are the different moments and what do they mean?
- What is skewness?
- Different kinds of proving convergence.
Calculus
Calculus is a large topic. Click the prior link to see a more complete set of notes on the topic for a brief introduction/review.
Questions
-
What is a derivative?
The derivative of a function \(f(\cdot)\) at point \(x\) is the instantaneous slope of the function at \(x\). \[\frac{d}{dx} f(x) = \lim_{dx->0} \frac{f(x+dx) - f(x)}{dx}\]
Because the derivative is a function, the derivative can be continued to be taken to second, third, etc… order derivatives each representing the rate of change of the prior.
-
What is the gradient?
The gradient can be seen as a linear operator on a function which maps \(f: \numfield^n \rightarrow \numfield^k\) where \(n, k > 0\). This linear operator applies a partial derivative for each basis in the vector.
-
Common rules of derivation.
\[\nabla_{\xvec} f(\xvec)g(\xvec) = f(\xvec) \nabla_{\xvec} g(\xvec) + g(\xvec) \nabla_{\xvec} f(\xvec)\]
\[\nabla_{\xvec} (f \circ g)(\xvec) = \nabla_g f(g(\xvec)) \nabla_{\xvec}g(\xvec)\]
Implicit differentiation is finding the derivative of functions or variables when there isn’t a clear form like \(y=f(x)\). This is best explained through an example. We want to find the derivative \(\frac{dy}{dx}\) from the function \(x^2 + y^2 = 1\).
If we can solve for \(y\) (which would be simple here \(y = \mp \sqrt{1 - x^2}\)) this can be done easily. But for this example lets assume we cant. Instead, we can take the derivative from the starting function
\begin{align*} \frac{d}{dx} (x^2 + y^2) &= \frac{d}{dx} (1) \quad &\text{Take the derivative.}\\ 2x + 2y \frac{dy}{dx} &= 0 \quad &\text{Distribute the derivative.}\\ \frac{dy}{dx} &= -\frac{x}{y} \quad &\text{Solve for $\frac{dy}{dx}$} \end{align*}
-
What is the derivative of common functions: e.g., e^x, sin(x), log(x)
\[\partialderiv{}{x} x^n = nx^{n-1} \quad \triangleright \quad n \neq 0, n\in\reals\] \[\partialderiv{}{x} e^x = e^x\] \[\partialderiv{}{x} a^x = \ln(a)*a^x \quad \triangleright \quad a > 0\] \[\partialderiv{}{x} \ln(x) = \frac{1}{x}\] \[\partialderiv{}{x} \log_{a}(x) = \frac{1}{x\ln(a)} \quad \triangleright \quad a > 0\] \[\partialderiv{}{x} \sin(x) = \cos(x)\] \[\partialderiv{}{x} \cos(x) = -\sin(x)\]
-
What is the derivative of the `relu` function?
The derivative of the \(relu(x)\) function is split into three parts.
-
\(x < 0\) \[\frac{d}{dx}relu(x<0)=0\]
-
\(x = 0\) This is a non-differential point in the function. Here we can use a subderivative at the differential point. We choose to include this with the first part of the function where the derivative is \[\frac{d}{dx}relu(x=0)=0.\]
-
\(x > 0\) \[\frac{d}{dx}relu(x>0)=1\]
-
-
What is the jacobian and the hessian?
Given a vector field \(\Fmat : \Amat \subset \reals^n \mapsto \reals^n\) we can apply the gradient operator several ways. The Jacobian is the outer product of the gradient operator and the vector field.
\[\text{The Jacobian: } \jacobian \defeq \nabla \otimes \Fmat = \left[\partialderiv{\Fmat}{x_1}, \cdots, \partialderiv{\Fmat}{x_n}\right] = \left[\begin{array}{ccc}{ \frac{\partial \Fmat_{1}}{\partial x_{1}}} & {\cdots} & {\frac{\partial \Fmat_{1}}{\partial x_{n}}} \\ {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial \Fmat_{m}}{\partial x_{1}}} & {\cdots} & {\frac{\partial \Fmat_{m}}{\partial x_{n}}} \end{array}\right]\]
Given a function \(f: \reals^n \mapsto \reals\) the Hessian is the jacobian of the gradient of \(f\).
\[\nabla \otimes \nabla f(\xvec)\]
-
What is the integral?
We can define an integral through a Riemannian sum: \[\int_a^b f(x) dx = \lim_{k\rightarrow\infty} \sum_k f(x+k\delta x)\delta x\]
where k is the number of sub intervals we break up range \([a, b]\).
-
Common integral tricks:
-
By parts \[\int udv = uv - \int v du \]
an example of \(\int ln(x) dx\):
\begin{align*} \int ln(x) dx = \int ln(x) 1 dx \\ u = ln(x) \quad du = \frac{1}{x} dx \\ dv = 1 dx \quad v = x \\ \int ln(x) dx = xln(x) - \int \frac{x}{x} dx \\ \int ln(x) dx = xln(x) - x + C \end{align*}
- By substitution
-
-
How do we estimate the value of an integral?
- Riemman sum with finite \(k\).
-
Fundamental theorem of calculus
If \(f(x)\) is continuous over an interval \([a, b]\), and the function \(F(x)\) is defined by \[F(x) = \int_a^b f(t) dt, \]
then \(\frac{d}{dx} F(x) = f(x)\) over interval \([a, b]\).
Linear Algebra
Linear algebra is the study of linear maps on finite-dimensional vector spaces. While this section covers some basics, a more detailed set of notes can be found in Linear Algebra.
A scalar \(x\in\numfield\) is a single element of a number field \(\numfield = \reals, \complexs, \ldots\).
#+being_definition A list of length \(n\in\naturals\) is an ordered collection of \(n\) elements separated by commas and surrounded by parentheses. This looks like: \[(x_1, \ldots, x_n).\] Two lists are equal if and only if they have the same length. #+end_definition
Using the definition of list above, we can define the set of all lists of length \(n\) of elements from \(\numfield\). \[\numfield^n = \{(x_1, \ldots, x_n): x_j \in \numfield for j = 1, \ldots, n \}\]
A vector space is a set \(V\) along with an addition on \(V\) and a scalar multiplication on \(V\) such that following properties hold:
- commutativity: \(u+v = v+u \quad\forall u, v \in V\)
- associativity: \((\uvec+\vvec) + \wvec = \uvec + (\vvec+\wvec)\) and \((ab)\vvec = a(b\vvec)\) for all \(\uvec,\vvec,\wvec\in V\) and all \(a, b \in \field\).
- additive identity: there exists an element \(0\in V\) such that \(\vvec + 0 = \vvec\) for all \(\vvec \in V\)
- additive inverse: for every \(\vvec \in V\), there exists \(\wvec\in V\) such that \(\vvec + \wvec = 0\)
- multiplicative identity: \(1\vvec = \vvec \quad \forall \vvec\in V\)
- distributive properties: \(a(\uvec + \vvec) = a\uvec + a\vvec\) and \((a+b)\vvec = a\vvec + b\vvec\) for all \(a,b\in\numfield\) and all \(\uvec,\vvec \in V\).
While I’ve defined some basics above, there is a lot to the intricacies of vector spaces and their interactions with linear maps and transformations. In the following, we will take the above for granted and deal with details more specific to basic machine learning and deep learning taken from (Goodfellow, Bengio, and Courville 2016). We will primarily focus on vector spaces on the field \(\reals\), while most of the content translates to \(\complexs\).
A vector \(\vvec \in V\) is a element of a vector space \(V\). We will use the convention that all vectors are column vectors. \[ \xvec = \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n\\ \end{matrix} \]
with the usual coordinate basis.
Different properties of a matrix
The properties of a matrix include:
- Definiteness
- Diagonality
- Upper or Lower Triangular
- block matrices
- Eigenvalues
What is a cross product
The cross product between two vectors
What is linear independence
A set of vectors are said to be linearly independent if there is no non-trivial linear combination which results in the zero vector. \[ \sum_i a_i \vvec_i = 0 \quad \text{Where $a_i \neq 0 \exists i$} \]
This means that there is one, say \(a_1\neq0\), scalar not equal to zero. Which means we can trivially rewrite the equation above: \[ \vvec_1 = \sum_{i=2}^n a_i \vvec_i \]
What is an eigenvector and an eigenvalue
An eigenspace of a matrix \(E_\lambda(\Mmat)\) is a vector space which contains the vectors (eigenvectors) which are scaled but not rotated by the linear transformation represented by \(Mmat\). Specifically, \[ \Mmat\vvec = \lambda\vvec \]
Above \(\vvec\) is called an eigenvector of \(\Mmat\) and \(\lambda\) is an eigenvalue (which is the amount the linear transform scales \(\vvec\)).
SVD
SVD is a matrix decomposition which exists for all rectangular matrices. It decomposes a matrix into three components: \[\Mmat = \Umat\Sigmamat\Vmat^*\] where \(\Vmat^*\) is the conjugate transpose of \(\Vmat\) (for real matrices \(\Vmat^* = \Vmat^\trans\)).
- \(\Umat\) is a complex unitary matrix.
- \(\Sigmamat\) is a \(m\times n\) rectangular diagonal matrix with non-negative real numbers on the diagonal.
- \(\Vmat\) is a complex unitary matrix.
Nice to think about properties of matrices in terms of their SVD decomposition.
Inverse of a matrix, Pseudo inverse of a matrix
The inverse of a matrix is defined as \[AA^\inv = I\] where \(I\) is the identity matrix. A matrix is invertable if and only if it is not singular (i.e. its determinant is zero).
Misc Math Concepts
- Monte Carlo methods to approximate \(\pi\).
Computer Science
Sorting Algorithms
-
Merge Sort
Merge sort uses the principle of divide and conquer. Where we break apart the list into a series of smaller lists to sort and then merge together. The steps are as follows:
- Divide the unsorted list into n sublists, each containing one element.
- Repeatedly merge sublists to produce new sorted sublists until there is only one sublist remaining. This will be the sorted list.
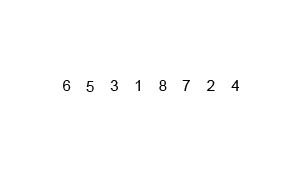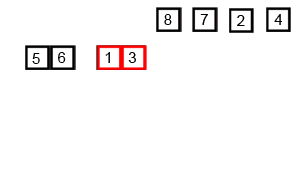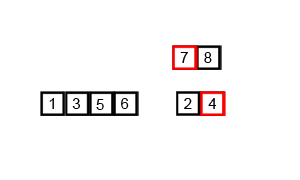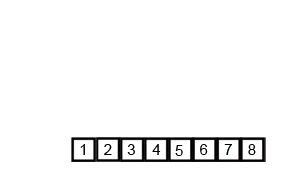
Figure 1: Merge Sort in action
There is another variant of merge sort called natural merge sort where which dividing the list you maintain sublists that are already sorted. This variant is said to be runs-optimal.
The merge sort algorithm has an average and worst-case performance of \(\bigoh(n \log n)\)
-
quicksort
Quicksort is an in-place sorting algorithm. The procedure is as follows:
- If the range has fewer than two elements, return immediately.
- Pick a value, called a pivot, that occurs in the range (exact method depends on the routine, and can involve randomness)
- Partition the range: reorder its elements so that all elements with values less than the pivot come before the division, while all elements with value greater than the pivot come after.
- Recursively apply the quicksort to the sub-range up to the point of division and to the sub-range after it.
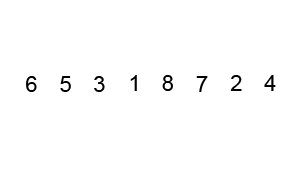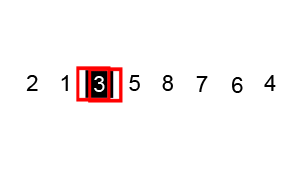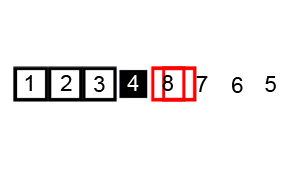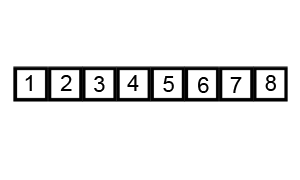
Figure 2: Quicksort in action! (From wikipedia)
Worst-case of this algorithm is when the most unbalanced partition occurs (i.e. when the list is sorted, or reverse sorted). This will result in \(\bigoh(n^2)\). The average case is \(\bigoh(n \log n)\) and the best case is \(\Omega(n)\).
- push sort
Big-Oh analysis
Look for loops!
Halting Problem
This is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running or continue to run forever. This is a decision problement about the properties of computer programs on a fixed turing-complete model of computation (i.e. all programs that can be written in some given programming language that is general enough to be equivalent to a Turing machine).
Turing machine, tape, and turing complete
A system of data manipulation tools is said to be Turing complete if it can be used to simulate any Turing machine. A Turing machine is an abstract model of computation which uses a finite set of instructions to manipulate an infinite tape. On the tape are symbols which are manipulated through read and write instructions, one at a time.
More specifically a Turing machine contains:
- A tape divided into cells, one next to eachother, with each cell containing a symbol from a finite alphabet.
- A head that can read and write to a cell on the tape and move the tape left or right.
- A state register which stores the state of the turing machine (which is from a finite set of states)
- A finite table of instructions.
P, NP, P=NP
The general class of questions in which an algorithm can give an answer in polynomial time is “P” or “class P”. The class of questions in which an answer can be verified in polynomial time, but no algorithm is known to exist which provides an answer in polynomial time is known as “nondeterministic polynomial time” or NP.
It is unknown if P=NP, and is an open question in theoretical computation. It is widely believed that P\(\neq\)NP, but a proof has yet to be discovered.
NP-complete problems are the set of NP problems who can be reduced to any other NP problem and whose answer is still verifiable in polynomial time. NP-hard problems are those whose verification may not be polynomial. All NP problems can be reduced to NP-hard problems.
stack vs heap
The stack is a part of the computer’s memory which stores temporary variables created by a function. This storage is temporary, and when exiting the scope of a function the data will be deleted. A heap is used to store global variables, or dynamically allocated variables (i.e. non-static arrays). The heap is not automatically managed by the CPU like the stack.
Hash Tables
A hash table is a data-structure which hashes a key using a deterministic hashing function and then stores a value at the location associated with the hashed key. It is a mapping from keys to values. This effectively has constant time access and write.
Because the storage is finite, there will likely be hash conflicts. There are several ways to resolve this:
- Move one space forward until a free space is found
- Have each bucket point to a list of key-value pairs and either push or search through the list depending on the operation.
To maintain amoratized \(\bigoh(1)\) as the load factor (i.e. how many hash conflicts are expected) increases, one should resize the hashtable to one that is double the size and move all the objects. There are other methods as well including linear hashing or maintaining two hash functions.
Other Data Structures
- Binary Tree
- Vector
- Queue
- Stack
- Linked-List
dynamic programming
Dynamic programming is both a mathematical optimization as well as a computer programming technique. It refers to taking a large complex problem and breaking it down into simpler sub-problems and then recursively finding the solution to those problems.
Finding a Value Function using Dynamic Programming is simple using the Bellman Equation. See the
Threads vs Processes
A thread is a parallel execution tool which has a shared memory pool with other threads. A process by default has one thread. A process (created through fork or some other mechanism) is a parallel execution paradigm with a separate memory pool from the other processes.
Compiled, Interpreted, and JIT oh my
-
A compiled language is one which takes a program and converts it to machine code (through a series of steps including pre-compilation, compilation, linking, etc…) (C/C++, go, etc…).
-
An interpreted language is one which does not get compiled and instead runs through another program which reads the code during execution and “interprets” this code, meaning it links the code to already pre-compiled objects which are then run. (Python)
A JIT compiled language is one which is compiled during execution. Python has some characteristics which compiles objects just in time, and you can use NUMBA to do this. Julia is a better example of a JIT language.
Reading Stack-traces
- Remain calm.
- Read the error.
- Find the first line a stack-trace has user-defined code.
- Read the previous errors to investigate what might be going wrong.
- Solve problem, research error online, or use a debugging tool to investigate parameters to function that is throwing error.
Questions
- Different sorting algorithms
- Big O analysis of memory and computational complexity
- What is the halting problem
- What is a turing machine; when is something turing complete
- What is P, NP, P=NP
- Stack vs Heap
- Hash tables
- Dynamic programming
- Working with lists (singly vs doubly linked)
- Big-O, Big-theta, Big-Omega
- Binary search trees and access (best, worst, usual)
- Threads vs Processes
- Compiled vs Interpreted vs Just-in-time
- Reading Stack-traces
Languages
Python
C++
Julia
Machine Learning
Supervised, self-supervised, semi-supervised, unsupervised learning
Supervised Learning is the typical starting point for most people learning about machine learning. This is setup with a set of features \(\Xmat\) and a corresponding set of labels \(Y\) which can either be classes (leading to classification) or real values (leading to regression).
Unsupervised Learning only starts with a set of features \(\Xmat\), where the goal is to discover patterns from the data.
Semi-supervised Learning combines both Supervised Learning and Unsupervised Learning and has a set of features and labels as well as a collection of unlabeled examples. The goal is to use the unlabeled examples to learn about the data and then use the labeled examples to create an inference model.
Linear Regression
Linear regression is the simplest form of regression and is used to minimize the mean squared error (MSE). More specifically, we model the labels as a linear function with error \[ \yvec = \Xmat \wvec + \boldsymbol{\varepsilon} \] where,
\[\begin{align*} \yvec &= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} \\ \Xmat &= \begin{bmatrix} 1 & x_{11} & x_{12} & \ldots & x_{1p} \\ 1 & x_{21} & x_{22} & \ldots & x_{2p} \\ 1 & x_{31} & x_{32} & \ldots & x_{3p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \ldots & x_{np} \\ \end{bmatrix} \\ \boldsymbol{\varepsilon} &= \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{bmatrix}, \wvec = \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix} \end{align*}\]
The most commonly used technique is that of linear least squares. This procedure finds the global minima of the objective function
\begin{align*} L(D, \wvec) &= \lVert \Xmat\wvec - \yvec \rVert_2^2 \\ &= (\Xmat\wvec - \yvec)^\trans (\Xmat\wvec - \yvec) \\ &= \yvec^\trans\yvec - \yvec^\trans\Xmat\wvec - \wvec^\trans\Xmat^\trans\yvec + \wvec^\trans\Xmat^\trans\Xmat\wvec \end{align*}
Now taking the derivative and setting to zero we can find the global minimum at \[\wvec = (\Xmat^\trans \Xmat)^\inv \Xmat^\trans \yvec.\]
With the condition that \(\Xmat^\trans\Xmat\) is not singular (i.e. the determinant is \(0\)).
Logistic Regression
Logistic regression is probably the most well known generalized linear model combining the Bernoulli distribution and a sigmoid transfer function. The model can be summarized as follows:
- \(p(y|\xvec) = \text{Bernoulli}(\alpha(\xvec))\) with \(\alpha(\xvec) = \expected[Y|\xvec]\)
- \(\expected[Y|\xvec] = \sigma(\wvec^\trans \xvec)\) or \(\text{logit}(\expected[Y|\xvec] = \wvec^\trans \xvec)\).
Remember that the Sigmoid Function is defined as \[\sigma(x) = \frac{1}{1+e^{-x}}\]
The SGD update for the logistic regression is: \[\wvec = \wvec - \eta\left( \sigma(\xvec_i ^\trans \wvec) - \yvec_i\right)\xvec_i\]
Of course we can also use Maximum Likelihood Estimation (which actually will present as the Batch Gradient Descent optimizer.
Gradient Descent
Gradient descent is to most commonly used optimization technique in Machine Learning. Effectively, it is
Gradient Descent is a first-order iterative Optimization algorithm for finding local minimum in a differentiable function. For a function \(f(\thetavec)\), \(\thetavec \in \reals^n\), and learning rate \(\alpha_i \in \reals\)
\[ \thetavec_{k+1} = \thetavec_{k} + \alpha_{k+1} \nabla f(\thetavec) \]
Convergence Guarantees
What is guaranteed by our algorithms?
The usual guarantees are those of convergence to some minimum (either local or global) with some conditions on the function space considered and on the learning rate used (in the case of Batch Gradient Descent and SGD.
Typically, the more convex the manifold we are optimizing over is the better our guarantees.
Features
Features are the mysterious vector \(\xvec_i\) that has been used without definition in this note. This is a “representation” (through real-numbers) of the instance. I’m using representation, again pretty loosly. But it is a vector of real numbers that are used to build a model. They have a monumental effect on the quality of an inference machine. Some methods to “discover” features
- Neural Networks w/ Backpropagation
- Kernel Methods
- Tilecoding
- Bag-of-features
Bias and variance in learning
The trade-off between bias and variance is well documented in Machine Learning.
Generalization
The ability to perform well on previously unobserved inputs is called generalization
Over-fitting and Under-fitting
Regularization
Evaluating methods
- AUC
- ROC
- T-test
- Standard error, Standard deviation, quantiles and more!
Support Vector Machines
Kernel Methods
Artificial Neural Networks
Boosting
Boosting is using subsets of samples to create an ensemble of models and then combining the models together (reduces variance).
Bagging
Bagging is another ensemble method.
Ensemble methods
Combining many models together to form a better estimate:
- Random Forests (many decision trees)
- Boosting
- Stacking (uses logistic regression to find the best).
Principle Component Analysis
PCA is a Dimensionality Reduction technique that creates a linear projection operator which projects the data onto the space defined by the first k eigenvectors of the covariance (across features) matrix. This explains the majority of the variance responsible by the features. See PCA for more details.
Advanced Neural Network Examples
Questions
- What is the curse of dimensionality
- What is supervised, self-supervised, and semi-supervised learning? Give examples of each?
- What is the learning rate/step-size and how does it impact learning?
- How do you do dimensionality reduction
- What is cross-validation?
- What are T-tests, what is standard error, and standard deviation? When would you use each?
- What is the kernel trick?
- What is Logistic regression?
- What is KL Divergence?
- What is batch-normalization
- What is weight and layer normalization?
- What is least-squares method?
- What is the bias variance tradeoff
- Name some loss functions; when would you use them?
- What is AUC?
- What is ROC?
- What is boosting and bagging?
- What are ensemble methods?
- What is an autoencoder?
- Exploding and vanishing gradients
- Generative Models
- Over and under-fitting
- Convergence guarantees for different learning methods
- What is backpropagation?
- ANNs
- SVMs
- Kernel trick
Reinforcement Learning
- What is the problem of reinforcement learning?
- What is a value function?
- What is a policy?
- What is the exploration-exploitation problem in reinforcement learning?
- Name three ways to learn value functions and the different tradeoffs.
- What are some of the differences between sarsa and q-learning?
- What is off-policy prediction/learning?
- What is the deadly triad?
- How does the deadly triad effect deep learning?
- Model-based vs Model-free reinforcement learning.
- Components of a deep-q network.
- What is an eligibility trace and how does it effect learning?
- Forward vs Backward view of n-step updates.
- What are the components of a Markov decision process?
- What makes a MDP partially observable? How might we solve this?
- If you were to construct an Agent to solve an un-tested reinforcement learning setting what architecture would you choose?
- What types of inputs can I expect?
- What types of actions can I expect?
- What are the computational constraints?
- What is a policy?
HR/personality Interviews
- Elevator pitch on your research.
- What would you do if you had a personal conflict w/ your manager?
- What is your biggest flaw, and how does it effect your research?
Research Topics
- Successor features/representations.
- Options/Option Models
- Predictive Knowledge and General Value Functions
