reed2022generalist: A Generalist Agent

\( \newcommand{\states}{\mathcal{S}} \newcommand{\actions}{\mathcal{A}} \newcommand{\observations}{\mathcal{O}} \newcommand{\rewards}{\mathcal{R}} \newcommand{\traces}{\mathbf{e}} \newcommand{\transition}{P} \newcommand{\reals}{\mathbb{R}} \newcommand{\naturals}{\mathbb{N}} \newcommand{\complexs}{\mathbb{C}} \newcommand{\field}{\mathbb{F}} \newcommand{\numfield}{\mathbb{F}} \newcommand{\expected}{\mathbb{E}} \newcommand{\var}{\mathbb{V}} \newcommand{\by}{\times} \newcommand{\partialderiv}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\defineq}{\stackrel{{\tiny\mbox{def}}}{=}} \newcommand{\defeq}{\stackrel{{\tiny\mbox{def}}}{=}} \newcommand{\eye}{\Imat} \newcommand{\hadamard}{\odot} \newcommand{\trans}{\top} \newcommand{\inv}{{-1}} \newcommand{\argmax}{\operatorname{argmax}} \newcommand{\Prob}{\mathbb{P}} \newcommand{\avec}{\mathbf{a}} \newcommand{\bvec}{\mathbf{b}} \newcommand{\cvec}{\mathbf{c}} \newcommand{\dvec}{\mathbf{d}} \newcommand{\evec}{\mathbf{e}} \newcommand{\fvec}{\mathbf{f}} \newcommand{\gvec}{\mathbf{g}} \newcommand{\hvec}{\mathbf{h}} \newcommand{\ivec}{\mathbf{i}} \newcommand{\jvec}{\mathbf{j}} \newcommand{\kvec}{\mathbf{k}} \newcommand{\lvec}{\mathbf{l}} \newcommand{\mvec}{\mathbf{m}} \newcommand{\nvec}{\mathbf{n}} \newcommand{\ovec}{\mathbf{o}} \newcommand{\pvec}{\mathbf{p}} \newcommand{\qvec}{\mathbf{q}} \newcommand{\rvec}{\mathbf{r}} \newcommand{\svec}{\mathbf{s}} \newcommand{\tvec}{\mathbf{t}} \newcommand{\uvec}{\mathbf{u}} \newcommand{\vvec}{\mathbf{v}} \newcommand{\wvec}{\mathbf{w}} \newcommand{\xvec}{\mathbf{x}} \newcommand{\yvec}{\mathbf{y}} \newcommand{\zvec}{\mathbf{z}} \newcommand{\Amat}{\mathbf{A}} \newcommand{\Bmat}{\mathbf{B}} \newcommand{\Cmat}{\mathbf{C}} \newcommand{\Dmat}{\mathbf{D}} \newcommand{\Emat}{\mathbf{E}} \newcommand{\Fmat}{\mathbf{F}} \newcommand{\Gmat}{\mathbf{G}} \newcommand{\Hmat}{\mathbf{H}} \newcommand{\Imat}{\mathbf{I}} \newcommand{\Jmat}{\mathbf{J}} \newcommand{\Kmat}{\mathbf{K}} \newcommand{\Lmat}{\mathbf{L}} \newcommand{\Mmat}{\mathbf{M}} \newcommand{\Nmat}{\mathbf{N}} \newcommand{\Omat}{\mathbf{O}} \newcommand{\Pmat}{\mathbf{P}} \newcommand{\Qmat}{\mathbf{Q}} \newcommand{\Rmat}{\mathbf{R}} \newcommand{\Smat}{\mathbf{S}} \newcommand{\Tmat}{\mathbf{T}} \newcommand{\Umat}{\mathbf{U}} \newcommand{\Vmat}{\mathbf{V}} \newcommand{\Wmat}{\mathbf{W}} \newcommand{\Xmat}{\mathbf{X}} \newcommand{\Ymat}{\mathbf{Y}} \newcommand{\Zmat}{\mathbf{Z}} \newcommand{\Sigmamat}{\boldsymbol{\Sigma}} \newcommand{\identity}{\Imat} \newcommand{\epsilonvec}{\boldsymbol{\epsilon}} \newcommand{\thetavec}{\boldsymbol{\theta}} \newcommand{\phivec}{\boldsymbol{\phi}} \newcommand{\muvec}{\boldsymbol{\mu}} \newcommand{\sigmavec}{\boldsymbol{\sigma}} \newcommand{\jacobian}{\mathbf{J}} \newcommand{\ind}{\perp!!!!\perp} \newcommand{\bigoh}{\text{O}} \)

tags

Reinforcement Learning

source

https://arxiv.org/pdf/2205.06175

authors

Reed, S., Zolna, K., Parisotto, E., Colmenarejo, Sergio G\‘omez, Novikov, A., Barth-maron, Gabriel, Gim\’enez, Mai, …

year

2022

The Gato agent is a generalist agent with the base of a Transformer. This agent is trained in a supervised manner, taking in a interleaved sequence of tokenized observations, separator tokens, and previously sampled actions to product the next action.

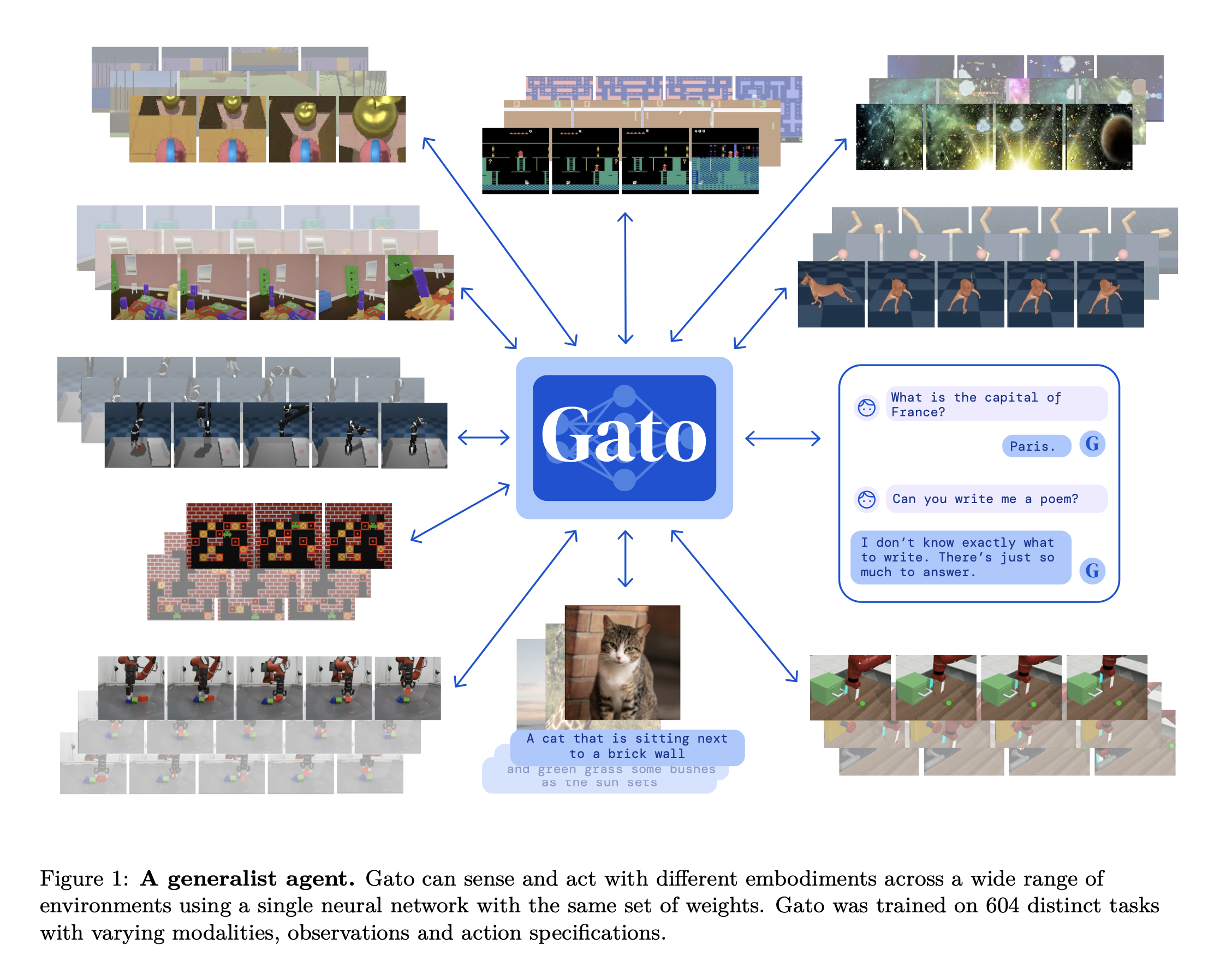
Architecture

Tokenization of inputs

• Text: Tokenization of the text information is done through (Kudo and Richardson 2018) with 32000 subwords. This results in a tokenization to integers of \([0, 32000)\).

• Images are tokenized through the same process as ViT. That is images are separated into 16x16 image patches ordered in raster order (i.e. the order of image rendering). Pixels are normalized to be in the range [-1, 1], and divided by \(\sqrt(16)\).

• Discrete values (e.g. Atari button presses) are flattened into sequences of integers. The range of the discretiztion is \([0, 1024)\).

• Continuous values are first normalized to [-1, 1] using \[ F(x, \mu=100, M=256) = \sign(x) \frac{\log(|x|\mu + 1.0)}{\log(M\mu + 1.0)} \] which results in the following normalization:

   These values are then discretized into 1024 bins with uniform width on the domain.

Network Architecture

The architecture has two main components

1. The parameterized embedding function which transforms tokens to token embeddings. This function works in two different modes depending on the token being embedded:
   • Text, discrete- or continuous-valued observations or actions are embedded via a lookup table into a learned vector embedding space.
   • Tokens belonging to image patches are embedded using a single ResNet block to obtain a vector per patch.
2. The Sequence model can work for next token prediction (i.e. a Transformer, specifically (Vaswani et al. 2017)).

GATO uses a 1.2B parameter decoder-only transformer with 24 layers, and embedding size of 2048, and a post-attention feedforward hidden size of 8196.

Training regime

Loss

Given the sequence of tokens \(s_{1:T}\) and \(\theta\), the loss function is:

\[ \mathcal{L}(\theta, \mathcal{B}) = - \sum_{b=1}^{|\mathcal{B}} \sum_{t=1}^{T} m(b, l) \log p_{\theta} \left ( s_l^{(b)} \left \vert s_1^{(b)} \ldots s_{l-1}^{(b)} \right. \right ) \]

where \(m(b, l) = 1\) when the token at index l is from text or a logged action, otherwise its \(0\).

Training data

The data used to train the agent. Below is a figure including full details of how much data is used to train the agent.

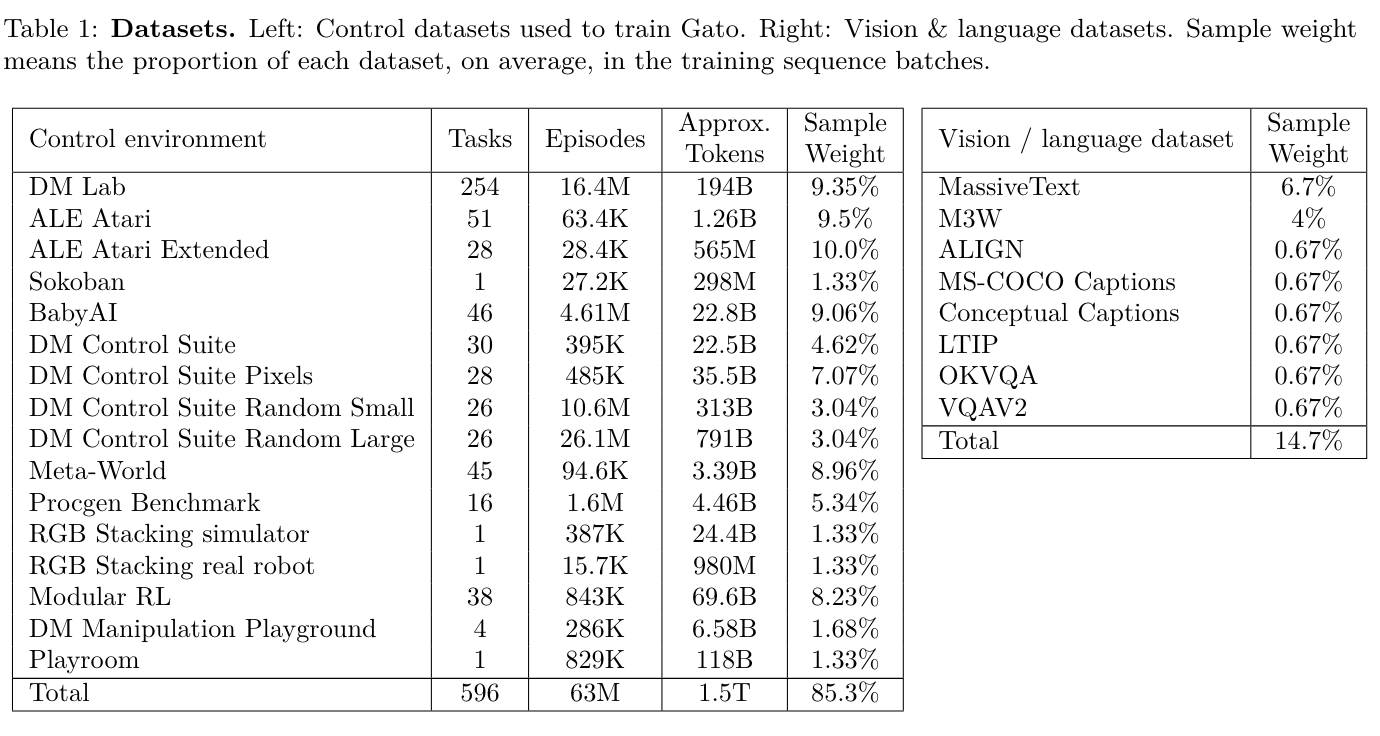
Different task types:

1. Simulated control tasks: Meta-world, Sokoban, BabyAI, DM Control Suite, DeepMind Lab, ALE.
2. Vision and language: Several datasets are used which have multi-modal image and text inputs as well as a dataset for text only preditcion.
   • MassiveText
   • ALIGN
   • LTIP
   • COCO
   • MultiModal MassiveWeb dataset
   • OKVQA
   • VQAv2
3. Robotics - RGB Stacking Benchmark: A robotoics benchmark for stacking objects. Both the simulated and real-world versions were used.

Results

References